- A+
在目前这个信息过载的星球上,文本的相似度计算应用前景还是比较广泛的,他可以让人们过滤掉很多相似的新闻,比如在搜索引擎上,相似度太高的页面,只需要展示一个就行了,还有就是,考试的时候,可以用这个来防作弊,同样的,论文的相似度检查也是一个检查论文是否抄袭的一个重要办法。
文本相似度计算的应用场景
- 过滤相似度很高的新闻,或者网页去重
- 考试防作弊系统
- 论文抄袭检查
光第一项的应用就非常广泛。
文本相似度计算的基本方法
文本相似度计算的方法很多,主要来说有两种,一是余弦定律,二是JaccardSimilarity方法,余弦定律不在本文的讨论范围之内,我们主要说一下JaccardSimilarity方法。
JaccardSimilarity方法
JaccardSimilarity说起来非常简单,容易实现,实际上就是两个集合的交集除以两个集合的并集,所得的就是两个集合的相似度,直观的看就是下面这个图。
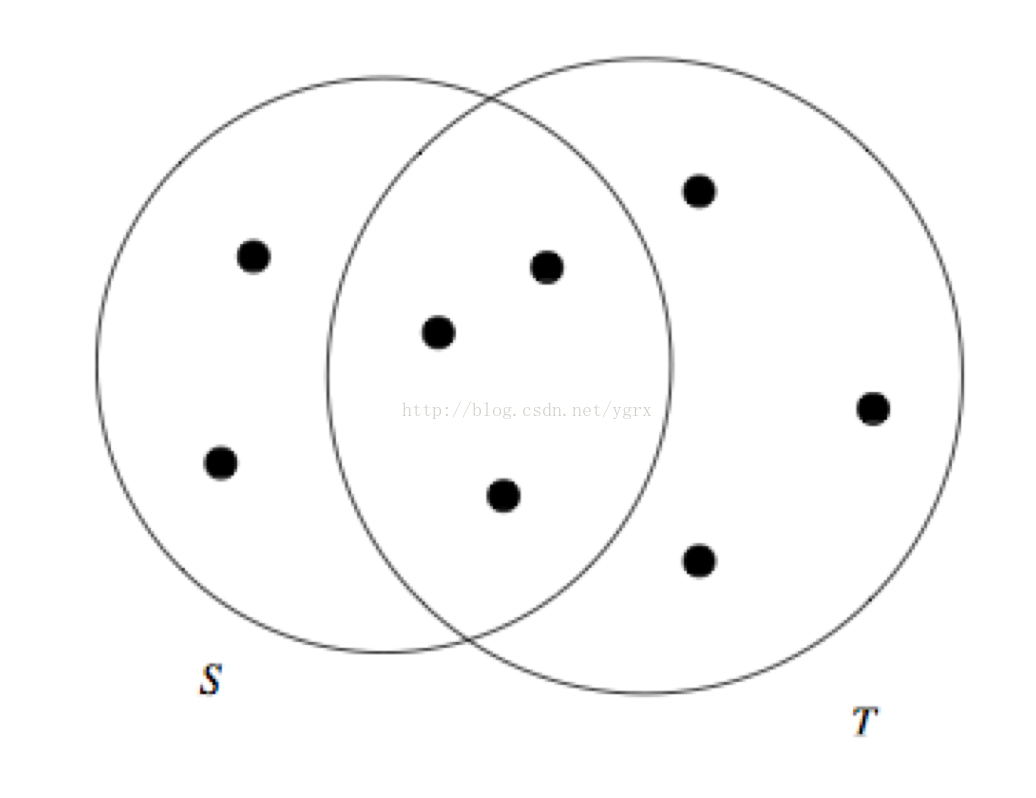
数学表达式是:
|S ∩ T|/|S ∪ T|
恩,基本的计算方法就是如此,而两个集合分别表示的是两个文本,集合中的元素实际上就是文本中出现的词语啦,我们需要做的就是把两个文本中的词语统计出来,然后按照上面的公式算一下就行了,其实很简单。
统计文本中的词语
关于统计文本中的词语,可以参考我的另外一篇博文一种没有语料字典的分词方法,文章中详细说明了如何从一篇文本中提取有价值的词汇,感兴趣的童鞋可以看看。
当然,本篇博客主要是说计算相似度的,所以词语的统计使用的比较简单的算法k-shingle算法,k是一个变量,表示提取文本中的k个字符,这个k可以自己定义。
简单的说,该算法就是从头挨个扫描文本,然后依次把k个字符保存起来,比如有个文本,内容是abcdefg,k设为2,那得到的词语就是ab,bc,cd,de,ef,fg。
得到这些词汇以后,然后统计每个词汇的数量,最后用上面的JaccardSimilarity算法来计算相似度。
具体的简单代码如下:
[python] view plain copy
- file_name_list=["/Users/wuyinghao/Documents/test1.txt",
- "/Users/wuyinghao/Documents/test2.txt",
- "/Users/wuyinghao/Documents/test3.txt"]
- hash_contents=[]
- #获取每个文本的词汇词频表
- for file_name in file_name_list:
- hash_contents.append([getHashInfoFromFile(file_name,5),file_name])
- for index1,v1 in enumerate(hash_contents):
- for index2,v2 in enumerate(hash_contents):
- if(v1[1] != v2[1] and index2>index1):
- intersection=calcIntersection(v1[0],v2[0]) #计算交集
- union_set=calcUnionSet(v1[0],v2[0],intersection) #计算并集
- print v1[1]+ "||||||" + v2[1] + " similarity is : " + str(calcSimilarity(intersection,union_set)) #计算相似度
完整的代码可以看我的GitHub
如何优化
上述代码其实可以完成文本比较了,但是如果是大量文本或者单个文本内容较大,比较的时候势必占用了大量的存储空间,因为一个词汇表的存储空间大于文本本身的存储空间,这样,我们需要进行一下优化,如何优化呢,我们按照以下两个步骤来优化。
将词汇表进行hash
首先,我们将词汇表进行hash运算,把词汇表中的每个词汇hash成一个整数,这样存储空间就会大大降低了,至于hash的算法,网上有很多,大家可以查查最小完美哈希,由于我这里只是为了验证整套算法的可行性,在Python中,直接用了字典和数组,将每个词汇变成了一个整数。
比如上面说的abcdefg的词汇ab,bc,cd,de,ef,fg,分别变成了[0,1,2,3,4,5]
使用特征矩阵来描述相似度
何为文本相似度的特征矩阵,我们可以这么来定义
- 一个特征矩阵的任何一行是全局所有元素中的 一个元素,任何一列是一个集合。
- 若全局第i个 元素出现在第j个集合里面,元素(i, j) 为1,否则 为0。
比如我们有world和could两个文本,设k为2通过k-shingle拆分以后,分别变成了[wo,or,rl,ld]和[co,ou,ul,ld]那么他们的特征矩阵就是
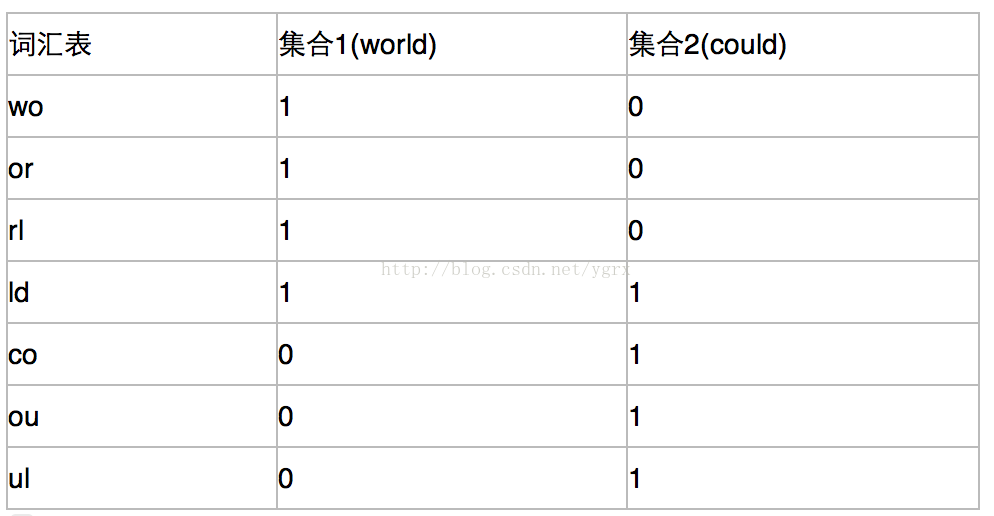
通过特征矩阵,我们很容易看出来,两个文本的相似性就是他们公共的元素除以所有的元素,也就是1/7
在这个矩阵中,集合列上面不是0就是1,其实我们可以把特征矩阵稍微修改一下,列上面存储的是该集合中词语出现的个数,我觉得可靠性更高一些。
至此,我们已经把一个简单的词汇表集合转换成上面的矩阵了,由于第一列的词汇表实际上是一个顺序的数列,所以我们需要存储的实际上只有后面的每一列的集合的数据了,而且也都是整数,这样存储空间就小多了。
继续优化特征矩阵,使用hash签名
对于保存上述特征矩阵,我们如果还嫌太浪费空间了,那么可以继续优化,如果能将每一列数据做成一个哈希签名,我们只需要比较签名的相似度就能大概的知道文本的相似度就好了,注意,我这里用了大概,也就是说这种方法会丢失掉一部分信息,对相似度的精确性是有影响的,如果在大量需要处理的数据面前,丢失一部分精准度而提供处理速度是可以接受的。
那么,怎么来制作这个hash签名呢?我们这么来做
- 先找到一组自定义的哈希函数H1,H2...Hn
- 将每一行的第一个元素,就是词汇表hash后得到的数字,分别于自定的哈希函数进行运算,得到一组新的数
- 建立一个集合(S1,S2...Sn)与哈希函数(H1,H2...Hn)的新矩阵T,并将每个元素初始值定义为无穷大
- 对于任何一列的集合,如果T(Hi,Sj)为0,则什么都不做
- 对于任何一列的集合,如果T(Hi,Sj)不为0,则将T(Hi,Sj)和当前值比较,更新为较小的值。
还是上面那个矩阵,使用hash签名以后,我们得到一个新矩阵,我们使用了两个哈希函数:H1= (x+1)%7 H2=(3x+1)%7 得到下面矩阵
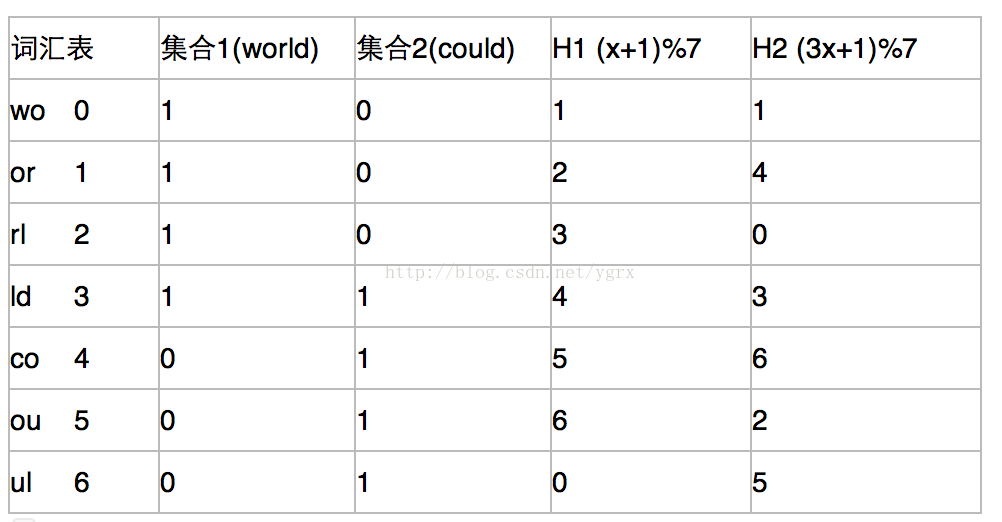
然后,我们建立一个集合组T与哈希函数组H的新矩阵
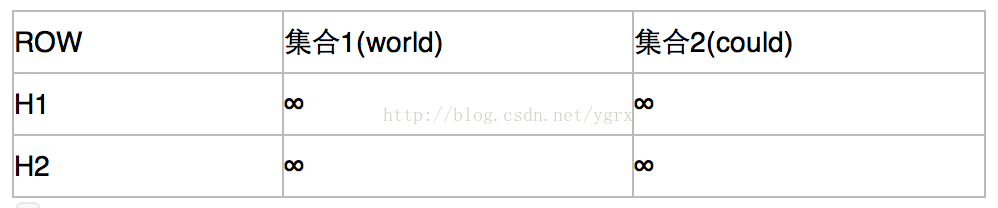
接下来,按照上面的步骤来更新这个矩阵。
- 对于集合1,他对于H1来说,他存在的元素中,H1后最小的数是1,对于H2来说,最小的是0
- 对于集合2,他对于H1来说,他存在的元素中,H1后最小的数是0,对于H2来说,最小的是2
所以,矩阵更新以后变成了
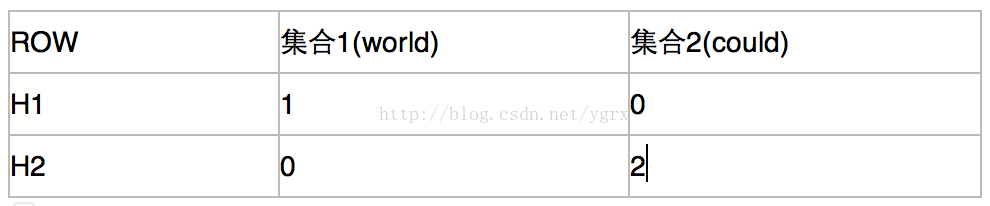
通过这个矩阵来计算相似度,只有当他们某一列完全相同的时候,我们才认为他们有交集,否则不认为他们有交集,所以根据上面这个矩阵,我们认为集合1和集合2的相似度为0。这就是我刚刚说的大概的含义,他不能精确的表示两个文本的相似性,得到的只是一个近似值。
在编程的时候,上面那个矩阵其实并不需要完全保存在内存中,可以边使用边生成,所以,对于之前用整体矩阵来说,我们最后只需要有上面这个签名矩阵的存储空间就可以进行计算了,这只和集合的数量还有哈希函数的数量有关。
这部分的简单算法描述如下:
[python] view plain copy
- res=[]
- for index1,v1 in enumerate(file_name_list):
- for index2,v2 in enumerate(file_name_list):
- g_hash.clear()
- g_val=0
- hash_contents=[]
- min_hashs=[]
- if(v1 != v2 and index2>index1):
- hash_contents.append(getHashInfoFromFile(v1)) #计算集合1的词汇表
- hash_contents.append(getHashInfoFromFile(v2)) #计算集合2的词汇表
- adjContentList(hash_contents) #调整hash表长度
- a=[x for x in range(len(g_hash))]
- minhash_pares=[2,3,5,7,11] #最小hash签名函数参数
- for para in minhash_pares:
- min_hashs.append(calcMinHash(para,len(g_hash),a)) #最小hash签名函数生成
- sig_list=calcSignatureMat(len(min_hashs)) #生成签名列表矩阵
- for index,content in enumerate(hash_contents):
- calcSignatures(content,min_hashs,sig_list,index) #计算最终签名矩阵
- simalar=calcSimilarity(sig_list) #计算相似度
- res.append([v1,v2,simalar])
- return res
同样,具体代码可以参考我的GitHub,代码没优化,只是做了算法描述的实现,内存占用还是多,呵呵

