- A+
继续以第一节的表1.5为例,我们做出如下的精简(如表1.7):
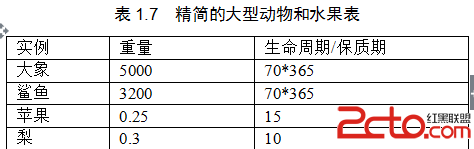
其中每个对象都是一个特征向量,从直觉上,我们可将其分为两大类:
大型动物:大象、鲨鱼
水果:苹果、梨
因为大象和鲨鱼都很大,生命周期也都很长,相比之下苹果和梨要小得多,保质期也都很短。很大、很长对很小、很短是在量上的比较,因此,利用初等数学的知识,这些给定数值的对象就可以看作一个n维坐标系下的点,并通过点与点之间的距离来度量。
两个向量之间的距离(此时向量作为n维坐标系中的点)计算,在数学上称为向量的距离(Distance),也称为样本之间的相似性度量(Similarity Measurement)。 它反映为某类事物在距离上接近或远离的程度,直觉上,距离越近的就越相似,越容易归为一类,距离越远就越不同,但这个直觉的标准是什么呢? 换句话说,这么划分的依据是什么呢?由此,我们引出向量间的各类距离公式,下面这些距离公式从不同角度对向量间的距离定义了衡量标准。
在引入距离公式之前,我们先看一个概念:
范数(来自百度百科): 向量的范数可以简单形象的理解为向量的长度,或者向量到坐标系原点的距离,或者相应空间内的两个点之间的距离。
向量的范数定义:向量的范数是一个函数||x||,满足非负性||x|| >= 0,齐次性||cx|| = |c| ||x|| ,三角不等式||x+y|| <= ||x|| + ||y||
L1范数: ||x||为x向量各个元素绝对值之和。
L2范数: ||x||为x向量各个元素平方和的开方,L2范数又称Euclidean范数或者Frobenius范数
Lp范数: ||x||为x向量各个元素绝对值p次方和的1/p次方
L∞范数: ||x||为x向量各个元素绝对值最大那个元素,如下:
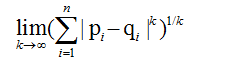
|
1
2
3
4
5
6
7
8
9
10
11
|
向量范数的运算:A = [8,1,6]# 手工计算modA = sqrt(sum(power(A,2)))print "modA:",modA# 库函数normA = linalg.norm(A)print "norm(A):",normA结果:modA: 10.0498756211norm(A): 10.0498756211 |

