- A+
对事物运动这种不确定性(随机性)的度量就是概率论,接下来我们考察一下概率的基本概念。衡量事物运动的随机性,必须从整体而不是局部来认知事物, 因为从每个局部,事物可能看起来都是不同的(或相同的)。不像其他的数学体系,这需要概率论架构在一套完整的数学模型之上。
为了更好的理解,我们修改一下上面的例子,假设我们的集合中只有苹果和梨两大类的对象,苹果有10个,梨也有10个,这次我们仅考察颜色特征。苹果有两种颜色:红色或黄色,其中红色占了8个;梨也有两种颜色:黄色或绿色,其中黄色占9个,假如从这堆水果中挑出一个黄色水果,问这个水果属于梨的可能性。
概率论基础概念:
样本(样本点):原指随机实验一个结果,可以理解为矩阵中的一个对象:苹果或梨;
样本空间:原指随机实验所有结果的集合,可以理解为矩阵的所有对象,引申为对象特征的取值范围:10个苹果,10个梨;
随机事件:是指样本空间的一个子集,可以理解为某个分类,它实际指向一种概率分布:苹果为红色;梨为黄色;
随机变量:可以理解为指向某个事件的一个变量:X{x=黄色}
随机变量的概率分布:给定随机变量的取值范围,导致某种随机事件出现的可能性,从机器学习的角度来看,就是符合随机变量取值范围的某个对象属于某个类别或服从某种趋势的可能性。
概率论妙处在于,由于随机性的存在,有时候无法直接讨论随机变量如何从样本空间映射到事件空间,因为随机变量的取值范围允许它可以映射到事件空间中的任一事件。此时,只有通过研究随机变量映射为每个事件的可能性,也就是说某个对象属于每个类别的可能性,才能做出合理的判断。理解了这一层也就理解了概率论的数学本质。
结合本例,我们不去研究黄色的苹果与黄色的梨有什么差别。而承认其统计规律:苹果是红色的概率是0.8,苹果是黄色的概率就是1-0.8=0.2,而梨是黄色的概率是0.9,将其作为先验概率。有了这个先验概率,就可以利用抽样,即任取一个水果,前提是抽样对总体的概率分布没有影响,通过它的某个特征来划分其所属的类别。黄色是苹果和梨共有的特征,因此,既有可能是苹果也有可能是梨,概率计算的意义在于得到这个水果更有可能的那一种。
这个问题的求解过程就是著名的贝叶斯公式:
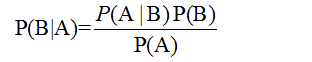
用数学的语言来表达,就是已知P(苹果)=10/(10+10),P(梨)=10/(10+10),P(黄色|苹果)
=20%,P(黄色|梨)=90%,求P(梨|黄色)
可得:P(梨|黄色)=P(黄色,梨)/P(黄色)
=P(黄色|梨)P(梨)/P(黄色)
=81.8%
贝叶斯公式贯穿了机器学习中随机问题分析的全过程。从文本分类到概率图模型,其基本原理都是贝叶斯公式,是机器学习领域最重要的基础概念。

