- A+
所属分类:其他杂项
理解了随机性和概率基础,下一步我们与之前介绍的矩阵结合起来,将它扩展到多维的情况。
矩阵是具有相同特征和维度的对象集合,其中每个对象,也称为行向量,都具有一个以上特征。如果,每个特征都用一个随机变量来表示,那么从概率论的角度,一个对象就可以表示为n个随机变量的整体,其中X=(X1,X2, …,Xn)为n维随机变量或随机向量。每个对象就是随机向量的一组取值,矩阵中的所有对象构成了随机向量的联合和边缘概率分布。
继续上一节的例子,我们把水果的种类和颜色都看作对象的两个特征,那么这个随机向量的联合概率分布可以写为(如表1.8):
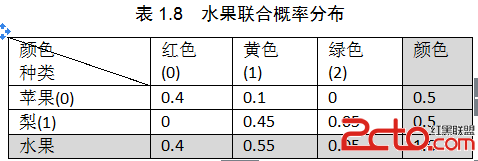
表中间白色部分是水果和颜色两个特征的联合概率分布,灰色部分是两个特征各自取值的边缘概率分布。形式上,以二维随机变量为例,X,Y的联合概率分布为:
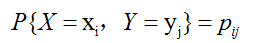

相应对象的边缘分布表示为:
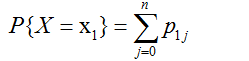
上例中,X=苹果的边缘概率分布为:
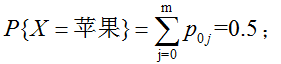
Y=绿色的边缘概率分布为: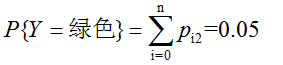
随机向量的联合概率分布和边缘概率分布描述了对象特征间的概率关系。机器学习中,对象以及对象构成的矩阵都是多元数据,因此,所有与概率相关的算法都以对象的联合概率分布和边缘概率分布为运算基础,本书中的多元统计算法有:朴素贝叶斯分析、回归分析、统计学习理论、聚类分析、主成分分析和概率图模型等等。

